This article will introduce us to Genetic Algorithms (GA). We will walk through the workings, representation, types and applications of the GA throughout this article. 

We hear about GA now and then, but what exactly is GA? And why does it sound so related to biology? Does it really use genes or some other biological entity while it is being implemented or the processes it comprises are like what happens in biology? These are some questions I had when I first heard about the term GA. This article is specially written for those who are new to the concept of GA and want to get a good grasp of the concept of GA in Computer Science (CS). 

The entire animal species, including today’s modern humans, did not appear on earth in one day. Millions of years of adaptation and evolution have evolved from the cave-dwelling primates to what we are today, Homo Sapiens. And the major driving force of this evolution is nature and environment. Nature is ever changing. Only nature selects all plants, animals and other natural elements in the changing environment. Numerous species of animals are extinct today because of natural selection alone. As the saying goes – ‘ Knowledge is the same, but the application of knowledge is different ‘. Therefore, the theory of natural selection and evolution not only points out the origin and existence of animals but also in the world of physical science, we have been able to use this theory in mathematical and scientific computation called genetic algorithms. This is a paltry attempt to explore the story of natural selection and the application of GA in real life.

Genetic Algorithm (GA) is a search-based optimization technique that follows the principle of Genetics and Natural Selection in the field of Biology. The main purpose of this algorithm is to find optimal or near-optimal solutions to quite a few difficult or difficult problems which are probably unsolvable or would take a very long time to solve using normal procedures or algorithms. Genetic Algorithm is quite often used to solve optimization problems in machine learning and to generate high-quality solutions for optimization problems. It is a subset of a much larger branch of computation, known as the Evolutionary Computation. GAs were developed by John H. Holland and his students and colleagues at the University of Michigan, of which David E. Goldberg is the most notable.

At year 1859. A book named ‘ On the Origin of Species ‘ was published. The author of the book is a British scientist Charles Darwin who recorded his experience after traveling the world for 5 years (~1831-1836) in the book. During his travels, he collected specimens of various species of organisms living in various islands of the Pacific Ocean and South America and later presented the results of research and experiments in a very simple language in his book. Through the book, Darwin introduced a new scientific approach to nature, philosophy of science, and in general to the origin and distribution of organisms, biodiversity, and evolution, which are fairly well-tested truths to the modern scientific community.

GA is a search heuristic that is inspired by Charles Darwin’s theory of natural evolution. This algorithm reflects the process of natural selection, where the fittest individuals are selected for reproduction in order to produce offspring of the next generation.

Discussing Darwin’s theory of natural selection requires a little bit of knowledge in biology. Every animal body comprises of many cells and the essential part of every cell is the nucleus. The nucleus of every animal cell contains chromosomes, and each chromosome contains many genes. Genes are sequences of chemical molecules called DNA. Genes handle the physical and behavioral characteristics of an animal. Cells of each species have a specific set of genes called genotype. The process of genetic combination of multiple animals of the same species is known as genetic recombination or crossover. It is through this genetic recombination that new offspring are created. On the other hand, mutation works behind the creation of animal diversity. Mutation is a random process that causes sudden changes in an organism’s genetic makeup. It created new species of animals through genetic mutation.

Now let’s look at natural selection through a common story that almost everyone uses.

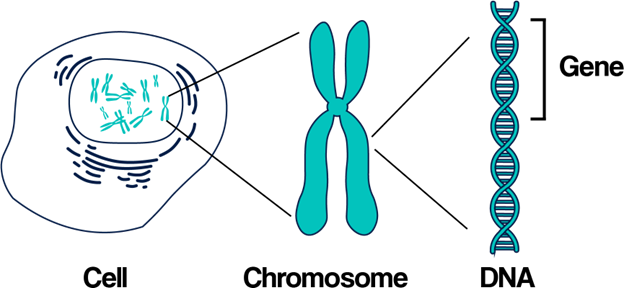
Figure: Basic building blocks of all living beings.
Reference: https://www.pngkey.com/maxpic/u2w7r5o0e6y3w7y3/

We all know the herbivorous (animals live on plants) giraffe. They live in areas where most of the trees are tall and have leaves high above the ground. As a result, giraffes living in these areas must have long necks to reach the leaves. We know 2 types of giraffe ancestors: the long-necked giraffe and the short-necked giraffe. Perhaps one type of mutation led to long-necked giraffes, and another type of mutation led to short-necked giraffes.

Naturally, giraffes with longer necks will be able to collect more food and have a higher chance of survival than giraffes with shorter necks. Not only that, but during the fight between themselves, giraffes with long necks will be ahead of giraffes with short necks. Similarly, long-necked giraffes will take part in more breeding and produce long-necked offspring than short-necked giraffes. On the other hand, short-necked giraffes will not survive due to lack of food and the production of these giraffes will decrease due to lack of reproduction. In this way, after a few generations, we will see that almost all members of the giraffe have long necks.

So the mutation that created the long-necked giraffe was a mutation that provided a survival advantage in nature. And because of another mutation, the short-necked giraffe became extinct because it could not survive in nature.

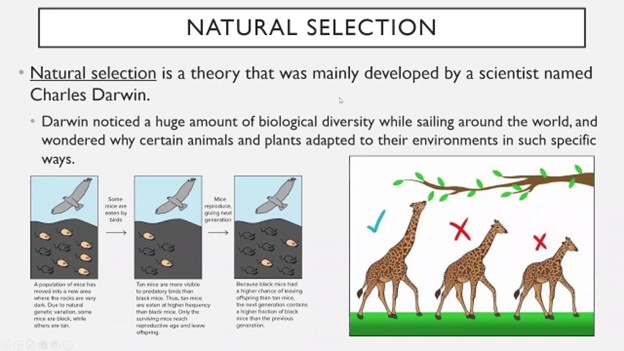
Figure: Natural Selection.

Reference: https://www.youtube.com/watch?v=V23Tu3akRbI

There are many other such examples of natural selection in animal history. The principle of Darwin’s theory is the same – that the evolution of species will continue from generation to generation through the correct modification of genes to adapt to nature and environment. It is essentially a ‘ survival of the fittest ‘ mechanism where only the fittest species survive.

The famous quote by Charles Darwin: “It is not the strongest of the species that survives, nor the most intelligent, but the one most responsive to change.”

The entire concept of genetic algorithms is based on the above quote.

Usually, GA is used when you do not know what the solution will be like. For instance, you want to create a car that can navigate through different terrains. You do not know how that car is going to look like, but you know the goal of the car. In this case, the GA can be used to make (i.e. generate/create the car too) the car to travel on different terrains, but the car design will be decided by the algorithm as well.

On the other hand, genetic programming is a specialization of genetic algorithms where each individual is a computer program. The main difference between genetic programming and genetic algorithms is the representation of the solution. Genetic Programming (or GP) introduced by Dr John Koza is a type of Evolutionary Algorithm (EA), a subset of Machine Learning (ML). EAs are used to discover solutions to problems that humans do not know how to solve, directly. GP is a systematic method for getting computers to automatically solve a problem and iteratively transform a population of computer programs into a new generation of programs by applying analogs of naturally occurring genetic operations. The genetic operations include crossover, mutation, reproduction, gene duplication, and gene deletion.

It starts with an initial set of programs composed of functions and terminals that may be handpicked or randomly generated. The functions may be standard arithmetic operations, programming operations, mathematical functions, or logical functions. The programs compete over given input and expected output data. Each program in the population is measured by how well it performs in a particular problem environment. This measurement is called a fitness measure. Top-performing programs are picked, then mutation and breeding are performed on them to generate the next generation. Next-generation competes with each other, the process goes on until the program is evolved to a proper one.

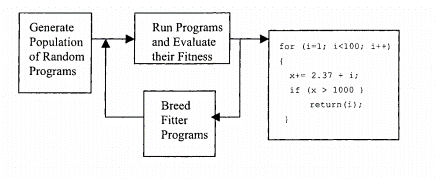
Figure: High level diagram of Genetic Programming.

Reference: https://www.researchgate.net/publication/2415604_A_Genetic_Programming_Tutorial/figures

In brief, Make an Initial population, Evaluation (assign a fitness function to each program in the population), Selection of ‘fitter’ individuals, Variation (mutation, crossover, etc), Iteration, and Termination. Programs in GP are expressed as syntax trees rather than as lines of code. Trees can be easily evaluated recursively. The tree includes nodes(functions) and links(terminals). The nodes show the instructions to execute and the demonstrate the arguments for each instruction.

The various types of Genetic Programming include:
1. Tree-based Genetic Programming
2. Stack-based Genetic Programming
3. Linear Genetic Programming (LGP)
4. Grammatical Evolution
5. Cartesian Genetic Programming (CGP)
6. Genetic Improvement of Software for Multiple Objectives (GISMO)

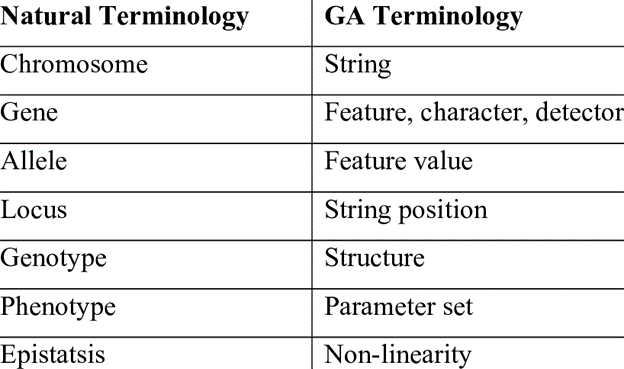
Figure: Natural Terminologies vs GA Terminologies.

Reference: https://www.researchgate.net/publication/265079036_CAD-BASED_DYNAMIC_LAYOUT_PLANNING_OF_CONSTRUCTION_SITES_USING_GENETIC_ALGORITHMS/figures?lo=1 

Reference : https://www.slideshare.net/AlaaKhamis/genetic-algorithms-81535698

Five phases are considered in a genetic algorithm.

1. Initial population: The process begins with a set of individuals called Population. An individual is characterized by a set of parameters (variables) known as genes. Genes are joined into a string to form a Chromosome (solution). In GA, the set of genes of an individual is represented using a string, in terms of an alphabet. Usually, binary values are used (string of 1s and 0s). We say that we encode the genes in a chromosome.

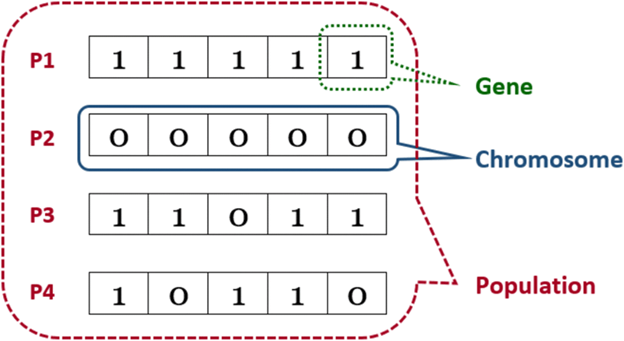
Figure: Population, Genes and Chromosomes.

Reference: https://www.researchgate.net/figure/Population-Chromosome-and-gene_fig14_342340658

2. Fitness function: The fitness function determines how fit an individual is (the ability of an individual to compete with other individuals). It gives a fitness score to each individual. The probability that an individual will be selected for reproduction is based on its fitness score.
3. Selection: The idea of the selection phase is to select the fittest individuals and let them pass their genes to the next generation. Two pairs of individuals (parents) are selected based on their fitness scores. Individuals with high fitness have more chance to be selected for reproduction.
4. Crossover: Crossover is the most significant phase in GA. For each pair of parents to be mated, a crossover point is chosen at random from within the genes. Offspring is created by exchanging the genes of parents among themselves until the crossover point is reached.

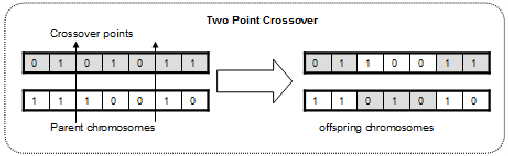
Figure: Crossover.

Reference: https://www.researchgate.net/figure/Two-point-crossover_fig2_220485962

5. Mutation: In certain new offspring formed, some of their genes can be subjected to a mutation with a low random probability. This implies that some of the bits in the bit string can be flipped.

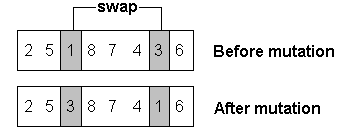
Figure: Before and after mutation.
Reference: https://www.researchgate.net/figure/Mutation-operator-The-genetic-algorithm-is-an-evolutionary-metaheuristic-It-is-an_fig3_342712750

The algorithm ends if the population has converged (does not produce offspring which differ significantly from the previous generation). Then it is said that the GA has provided a set of solutions to our problem.

Here is a simple walkthrough with an example of the entire process:

• Problem Domain: First of all, we have to define all the problems and the constraints that we are calling the problem domain. Suppose our problem scenario requires us to have 4 pair of numbers as a set. So, it can be something like {(2, 4), (3, 5), (1, 6), (7, 8)}. So here the question occurs: whether the numbers are only comprised of a single digit or not, whether it can have negative values and so on. That way we can define our problem domain.

• Possible Solutions (Ancestors): Suppose for that particular problem we got 12 solutions. Two of them are Solution 1 that we showed before i.e. {(2, 4), (3, 5), (1, 6), (7, 8)} and Solution 2: {(1, 4), (6, 8), (2, 4), (1, 5)} and so on. Here those two solutions will be called as genotype. And the individual values i.e. 1, 2, 3, 4, 5, 6, 7, 8 will be called parameters or genes.

• Fitness based Competent Solution: Now we can define a fitness function for our problem domain and get an outcome for all probable solution. Suppose for a particular fitness function we get a value of 12 for the first solution and 15 for the second one that showed earlier and so on for others. Now we have to select solutions based on the value achieved from the fitness function. There are lots of technique we can apply to select candidate solutions. We discussed them in the upcoming section. We are assuming we have chosen first two solutions that we have mentioned and have fitness value of 12 and 15. Other solutions are not fit by the selection method.

• Crossover: Now we will do crossover on the two solutions. We will define a crossover point, suppose that is 1. So after making a crossover, it will be like the figure below.

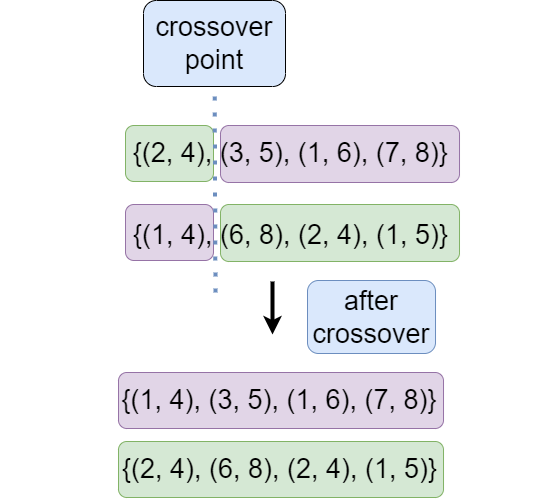
Figure: Crossover.

5. Mutation: After crossover, we can apply mutation, as crossover only produces characteristics of the parents. We can add random mutation occasionally to create mutated generation with unique characteristics. We can apply different controlled mutation like changing single parameters or multiple parameters, keeping values closer to the original one or with a huge difference.

GA is heavily inspired by the natural selection, so to see how GA work, we should actually investigate how natural selection work. To begin with, the working process of GA also starts by having an initial population. The primary stage is to calculate fitness. Calculate fitness can be considered as a part of the selection process as it basically used to calculate the “score” of each individuals to show whether its a strong individual or a weak one. All the strong entities then selected and passed to a stage called cross over, this stage is like the mating stage in the previous diagram. In this stage, 2 random parents is selected from the strong entity list to perform crossover. After performing crossover, a child is created and also mutated to add some variation to the gene. Finally, this child rejoin the population and the process repeats.

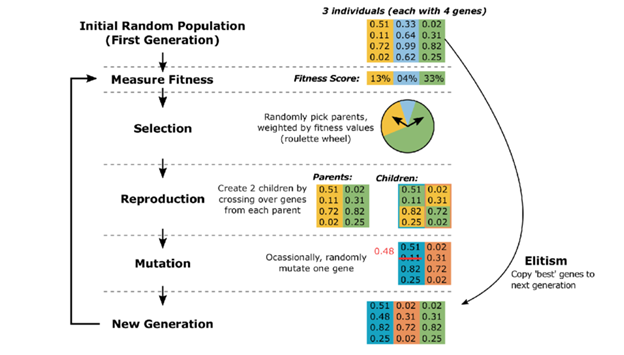
Figure: Basic building blocks of GA

Reference: https://www.researchgate.net/figure/Illustration-of-the-genetic-algorithm-concept-showing-an-example-iteration-of-the_fig3_305440735

Selecting appropriate solution is what the GA’s selection stage is all about. After calculating the fitness score, the next step is to use some methods to select a list of solutions that can later produce a better solution. Although we can create our own way of selecting the fitting solutions, there are some famous methods that we can use:

• Fitness proportionate selection
• Tournament selection
• Truncation selection
• Fitness uniform selection

 more methods can be found from here.

Crossover is the stage where selected solutions are combined to form new solutions. Just like the selecting stage, there are also many techniques of crossover and we can also find them here.

Similar to selection stage, in crossover stage, we can also invent our own crossover techniques, however, there are also some techniques that we can use:

• Single-point crossover
• Two-point crossover
• Uniform crossover
• Three parent crossover

To mutate a child, there are also a variety of techniques that we can use:

• Bit string mutation
• Flip Bit
• Non-Uniform
• Uniform

You can find more of them here.

After mutating the child, it will join back with another mutated child to reform a new population and the entire process starts over.

So when does it stop? The answer is extremely simple: when do we stop practicing typing on a keyboard with 10 fingers? When our typing skill is perfect, of course. Same thing with GA, the process will stop if a certain solution’s fitness reaches the desired fitness. 

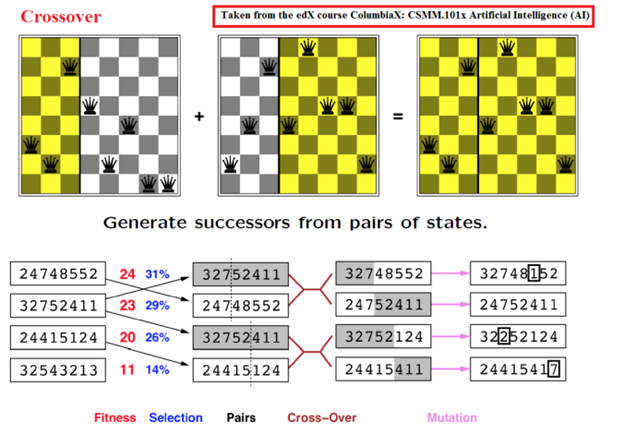
Figure: Solving N-Queen Problem with GA.

Reference: Attached in the Figure.

We will try to solve N-Queen problem with GA. So, N-Queen is a challenge where N queens have to be placed on an NxN chessboard in such a way that no queen is in the way of any other queen. The task is quite difficult as the queen is considered being the most powerful in chess. If you don’t believe it, you can try it now with a simple chess board. A typical chess board is 8 x 8 squares.

Population:

The set of solutions existing at any point in time is called Population. All our methods will be used on this population set.

Population Size:
The count of solutions there will be in the population in the initial state.

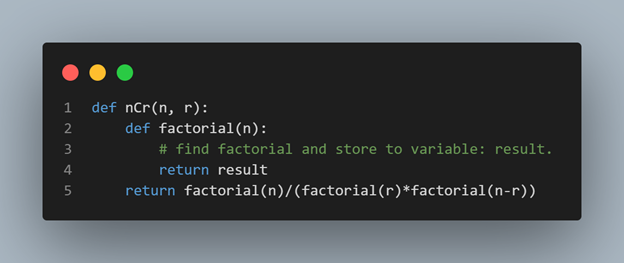
Maximum conflict: Number of conflict between Queens.
For 1 Queen on the board there will be 0 conflict,
for 2 Queen there will be 1 conflict,
for 3 there will be 3 conflicts (i.e. for Queen A,B,C; A-B, B-C, A-C) and so on.
We can find the conflicts count by achieving the combination of total Queen on the board, thus applying nCr where n = number of Queens on the board and r = 2.

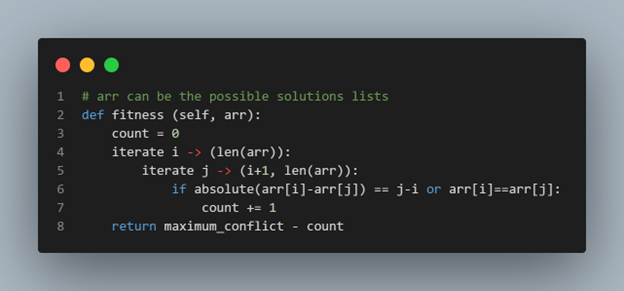
The expression of fitness for our chess program is how many Queens in a given solution are not in the path of any other Queen i.e. if the Queen’s conflict score for a solution is zero then that is the correct solution. We can design fitness functions in various ways. Best way to design a fitness function is to take smaller progress into account. Pseudo code below can be a solution of a fitness function for our setup.

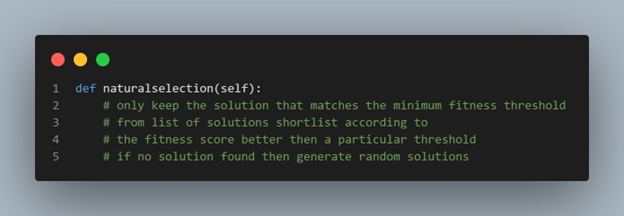
Natural Selection

Crossover

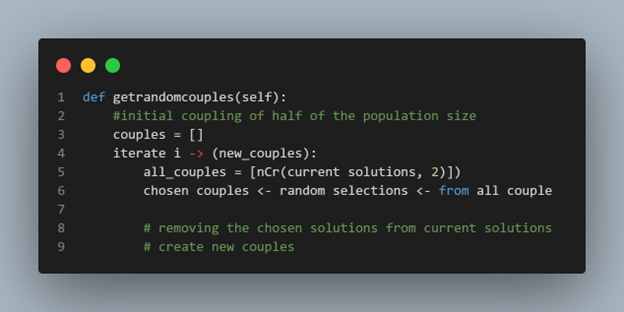
(DONE)

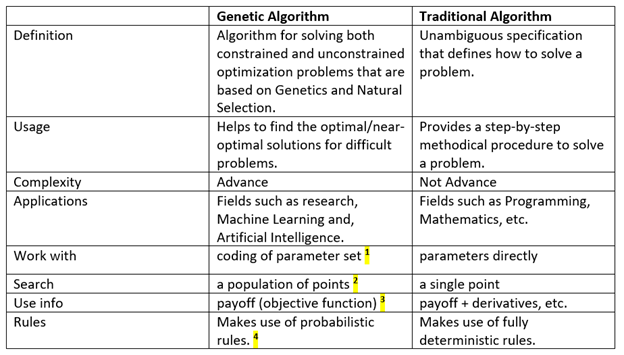
¹ GA deals with a coded form of the function values (parameter set), rather than with the actual values themselves. So, for example, if we want to find the maximum of a function f(x1, x2) of two variables, the GA would not deal directly with x1 or x2 values, but with strings that encode these values.

² GA uses a population of points to search, not just a single point on the problem space. This gives GA the power to search noisy spaces littered with local optimum points. Instead of relying on a single point to search through space, the GA looks at many different areas of the problem space at once and uses all of this information to guide it.

³ GA uses only payoff information to guide themselves through the problem space. Many search techniques need a variety of information to guide themselves. Hill climbing methods require derivatives, for example. The only information a GA needs is some measure of fitness about a point in the space (sometimes known as an objective function value). Once the GA knows the current measure of “goodness” about a point, it can use this to continue searching for the optimum.

⁴ GA is probabilistic‌, not deterministic. This directly results from the randomization techniques used by GA. Probabilistic — random population with random mating, crossover, and mutation.

GA is not a deterministic algorithm. It is a dynamic algorithm which is completely based on randomness. Hence, genetic algorithms work very well in problem domain with large search space subject to selection of proper fitness function. Knowing how it works in theory would require resonating the neurons in the brain with some of the most beautiful and complex mathematical manipulations that are beyond our scope.

Apart from robotics and artificial intelligence, genetic algorithms are used in various fields of biology and economics including Cryptographic Analysis, Game Theory, Optimum Network Routing System design in the world of computation. Also in software testing genetic algorithms are used to select optimum white box or structural test case (White-box/Structural Test Case) with mutation testing.

Other areas including,

1. Acoustics
Distinguish between sonar reflections and different types of objects. Design Active noise control systems which cancel out the undesired sound by producing sound waves that destructively interfere with the unwanted noise.

2. Aerospace Engineering
Design SuperSonic aircraft by minimizing aerodynamic drag at supersonic cruising speeds, minimizing drag at subsonic speeds, and minimizing aerodynamic load.

3. Financial Markets
To predict the future performance of publicly traded stocks.

4. Geophysics
Locate earthquake hypocenters based on seismological data.

5. Materials Engineering
Design electrically conductive carbon-based polymers known as polyanilines. Design exposure pattern for an electron lithography beam.

6. Routing and Scheduling
Find optimal routing paths in telecommunication networks that are used to relay data from sender to recipients.

7. Systems Engineering
To perform the multi-objective task of designing wind turbines used to generate electric power.

(DONE)

1. Population Selection Problem – 

Defining the population size and selecting the initial individuals can be a bit challenging.
2. Defining Fitness Function – 

To find out the optimal minimum or maximum value, we must define our fitness function in such a way so that optimal solution fitness can increase with every iteration.
3. Premature or rapid convergence of GA –
Rapid convergence is a very common as well as very general problem in GA. It occurs because the fitness function changes its value rapidly, resulting in a premature convergence.
There are several methods to modify our fitness function in such a way so that convergence occurs slowly which will allow enough time for GA to search in the whole space and find the global optima. Three ways are defined below:

i. F’ = a * F + b
F = normal fitness value of the population string.
a = small number
b = relatively larger number
Now it can be clearly seen that even if F rapidly increases then after F’ will increase
slowly.

ii.  F’ = a * (Fk)
k = constant number in (0,1)
So even if F increases rapidly it may not create rapid convergence.

iii.  F’ = a*(Fk)
k = func(t) , t = generation
Here fitness function is changed in each generation.

4. Convergence to Local Optima –
   Another important problem is that most of the time GA converges to local optima. We may think that we have found the optimal solution but actually, we didn’t. Now, it is important to note that GA’s ability to find the optimal solution lies in the user’s hand. An optimal solution will be achieved only if the programmer has written the code so that GA can search over the entire space to find the optimal solution. So what we should do in such a case is that we should change our crossover and mutation function because they are responsible for changing the population in each iteration.

That’s it. This is the end of this article. I hope that after reading it, you will have a better insight into Genetic Algorithms and its usage. Thanks.

• Adaptation in Natural and Artificial Systems ‘ by  Professor John Holland

• Koza, John R. 1992. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA: The MIT Press

• Introduction to Genetic Programming Tutorial Gecco-2010 — Portland, Oregon July 2010

• A Genetic Programming Tutorial John R. Koza and Riccardo Poli

• https://www.researchgate.net/publication/2415604_A_Genetic_Programming_Tutorial

• https://in.mathworks.com/help/gads/what-is-the-genetic-algorithm.html

• https://www.sciencedirect.com/science/article/pii/B9780124167438000051

• https://en.wikipedia.org/wiki/List_of_genetic_algorithm_applications

• https://youtu.be/N3tRFayqVtk